Motivation: Establishing communications in a multi-channel wireless network requires the communicating devices (two nodes in the case of unicast, and three or more in the case of multicast) to “rendezvous” on a common channel before carrying out normal data transmissions. The rendezvous process enables the exchange and negotiation of critical information, including transmission parameters (e.g., transmission powers, transmission rates, idle channels), connectivity and topological changes, timing information, etc. This process takes place at the time a new session is to be established and also following the loss of connectivity between the transmitter and receiver (e.g., due to jamming and/or fading conditions). Clock drifts make it difficult for the communicating parties to maintain a common time reference, so the rendezvous process must be robust to misalignment and asynchronous operation. Moreover, in a dynamic spectrum access (DSA) environment, rendezvousing may need to be conducted under a heterogeneous spectrum setting, i.e., the set of idle channels are generally different for different nodes. This heterogeneity is caused by spatiotemporal variations in spectrum availability (see Figure 1) as well as interference/jamming conditions.

 

A simple approach to rendezvous is to rely on a predetermined, statically assigned frequency channel (or a common spreading code). However, this approach is vulnerable to selective jamming attacks, in which a smart adversary specifically targets the rendezvous process in hope of creating a denial of communication (DOC) attack. The adversary may discover the “rendezvous channel” (or code) by chance, through public knowledge of the underlying protocol semantics, or by compromising one of the network devices. Furthermore, for DSA systems, relying on a predetermined rendezvous channel is not even an option. An alternative approach for rendezvous is to use random frequency hopping (FH). In this case, the communicating parties hop independently until they meet each other. While this approach is robust to insider attacks, it suffers from a long time-to-rendezvous (TTR), particularly in the case of multicast rendezvous (where several nodes need to simultaneously meet at the same time slot over the same frequency channel). It also does not account for spectrum heterogeneity in DSA systems.

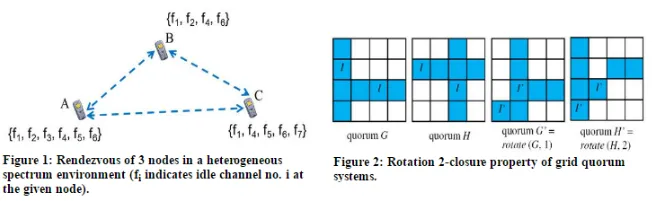
Recently, researchers have considered a structured approach for designing FH-based rendezvous sequences based on the concept of quorums. In plain terms, a quorum system is a collection of nonempty sets (called quorums) that pairwise overlap by one or more elements. For example, Q ={{3,4},{2,3},{2,4}} is a system of three quorums: {3,4}, {2,3}, and {2,4}. One important advantage of quorum-based FH designs is their robustness to synchronization errors. In particular, certain quorum systems enjoy the rotation k-closure property, whereby any misalignment between any k quorums of the underlying quorum system results in k rotated quorums that also pairwise overlap. Figure 2 shows the rotation 2-closure property for a 4-by-4 grid quorum system. In a grid quorum system, each FH sequence is divided into frames, each frame consisting of several time slots. The slots in a frame are arranged into a square grid (e.g., a 4-by-4 grid in Figure 2). Each node selects a column and a row from the grid, representing the quorum of that node (the blue cells in Figure 2). The slots that correspond to the selected quorum are assigned a channel called the rendezvous channel and the remaining slots are assigned a random channel. The two nodes are guaranteed to rendezvous during the common quorum slots, indicated by the letter I in the two leftmost subfigures. Rotating either or both quorums still results in common quorum slots (indicated by the letter I' in the two rightmost subfigures). The k-closure property is a key to achieving rendezvous even when devices are not time-synchronized.

On the other hand, due to their systematic design, quorum-based schemes are inherently vulnerable to jamming attacks, particularly when the attack is launched by an insider node, e.g., when a trusted node has been compromised and its secrets have been partially or completely revealed to the attacker. In this case, the attacker can exploit his knowledge of the underlying quorum system to launch a DOC attack.

Research Trusts

1. Asynchronous Unicast Rendezvous for DSA Systems

In this thrust, we consider the rendezvous of two nodes in an asynchronous spectrum-heterogeneous DSA environment. We user quorum systems to design the FH sequences of the two nodes. One approach that we have explored relies on nested grid quorums, whereby multiple grid quorums of different sizes are used in each FH sequence. The objective of this nested design is twofold. First, this nested design expedites the rendezvous process (i.e., reduces the TTR), especially in the presence of fast primary user (PU) dynamics. This is done by: (i) increasing the average number of rendezvous slots in a frame, and (ii) implementing multiple rendezvous channels, so if one channel is occupied by a PU, other channels can still be used for rendezvous. The second goal of our nested design is to provide higher resiliency to insider attacks. More specifically, in the nested design, each FH sequence involves multiple quorums of different sizes, which makes it harder for an insider adversary to infer the FH sequence by only knowing the general structure of the underlying grid quorum system.

 

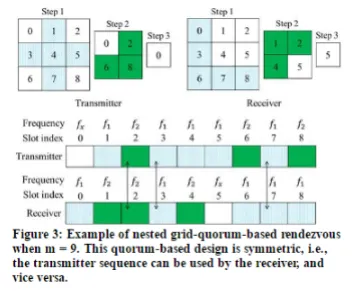
The following example illustrates the general idea of the nested quorum design. Consider the construction of one FH sequence. Suppose that this sequence is composed of successive frames, each of length m=9 slots. This frame length corresponds to a 3-by-3 grid quorum system. It results in a nesting degree of two (i.e., two rendezvous channels per frame). Let Zn denote the set {0,2,...,n-1} for any positive integer n. Then, each FH sequence is obtained as follows:

Step 1: Construct a grid quorum system Q under Z9. Q has 9 different quorums, each containing 2√ 9 - 1 = 5 slots that comprise one row and one column of the 3 × 3 grid (see Figure 3).

Step 2: For each frame j in the FH sequence, j=1,2,...,:

• Select the outermost quorum G1(j) of frame j from Q (e.g., G1(j) = {1, 3, 4, 5, 7}, where each element represents the index of a time slot in a 9-slot frame).
• Assign a rendezvous channel h1(j) to the slots that correspond to G1(j). This h1(j) is called the outermost rendezvous channel.
• Prune quorum G1(j) from the original 3 × 3 grid and select the next outermost quorum G2(j) from the resulting 2 × 2 grid (e.g., G2(j) = {2, 6, 8}). Then, assign another rendezvous frequency h2(j) to the slots that correspond to G2(j).
• Assign a random frequency hx(j) to each of the remaining unassigned slots in the frame.

The above procedure is applied independently to other FH sequences (one per node).

 

Research issues that are being adressed include:

• Selection of rendezvous channels - We are developing mechanisms for selecting the rendezvous channels (e.g., channels h1(j) and h2(j) in Figure 3), depending on the predicted PU dynamics.
• Quorum selection - We are investigating mechanisms for selecting the quorums in Q (e.g., G1(j) and G2(j) in Figure 3) given that the rendezvous channels have already been selected. This selection is done based on the expected behavior of PUs in the next frame as well as the expected number of rendezvous slots. Note that while any two outermost quorums are guaranteed to overlap, this is not necessarily true for the inner quorums. The selection of certain outermost quorums impacts the expected number of rendezvous slots for the inner quorums.
• Studying other quorum systems - We are considering other types of quorum systems as candidates for FH-based rendezvous. These include torus and cyclic quorum systems.
• Implementation and experimental evaluation - Besides analysis and simulation-based studies, we also plan to implement several of the developed rendezvous protocols using NI-USRP experimental radios and evaluate their performance experimentally.

2. Asynchronous Multicast Rendezvous for DSA Systems

In this thrust, we study multicast rendezvous. Our objective is to enable a node (called the multicast initiator) to convey a critical message simultaneously to all other nodes in a multicast group, i.e., all receiving nodes must securely receive the same message at the same time. Under this requirement, implementing the multicast rendezvous as a series of unicast rendezvous is not an option.

It turns out that grid quorum systems used for the unicast case cannot be used for multicast rendezvous because these systems can only guarantee pairwise overlap between quorums but not necessarily overlap between a set of k quorums (k>2). Accordingly, we are looking into other quorum systems that can support multicast rendezvous. The candidates under consideration exhibit different characteristics in terms of speed of rendezvous (i.e., TTR) and security. Other features of interest include energy efficiency, expressed in the number of required transmissions for successful rendezvous. Two examples of our recently studied quorum systems for multicast rendezvous are:

 

Uniform k-arbiter Quorum System: This quorum system enjoys the (k+1)-intersection property, meaning that it guarantees overlap between any k+1 quorums. It also satisfies the rotation k-closure property, described before. These features enable such a quorum system to achieve asynchronous multicast rendezvous. Figure 4 shows a uniform 2-arbiter quorum system Q = {{0,1,2},{0,1,3},{0,2,3},{1,2,3}}. Any three quorums (i.e., subsets) overlap in one element. Note that the length of the complete set (i.e., {0,1,2,3}) is short. In order to have a uniform 2-arbiter quorum system where any 3 quorums overlap, we need a set of size 4. The size of the complete set is essentially the frame length in the resulting FH sequences. This means that the k-arbiter quorum system can achieve rendezvous within one frame length, irrespective of any misalignment. However, as can be seen from Figure 4, the subsets (quorums) in the uniform k-arbiter quorum system are close to each other, i.e., the Hamming distance (HD) between them is small. This degrades the performance of such quorum systems in presence of node compromise.

Chinese Remainder Theorem (CRT) Quorum System: Figure 5 shows an example of a CRT quorum system Q that consists of 3 quorums: Q = {{0,2,4,6,8,10,12,14,16,18,20,22,24,26,28},{0,3,6,9,12,15,18,21,24,27},{0,5,10,15,20,25}}. In contrast to the uniform k-arbiter quorum system, the length of the complete set in the CRT quorum system is relatively long. Therefore, the frame length (and hence the TTR) is long. For example, the length of the complete set of a CRT quorum system of three quorums is 30. On the other hand, the HD between different quorums in a CRT quorum system is high, which makes such quorums very resilient to node compromise.

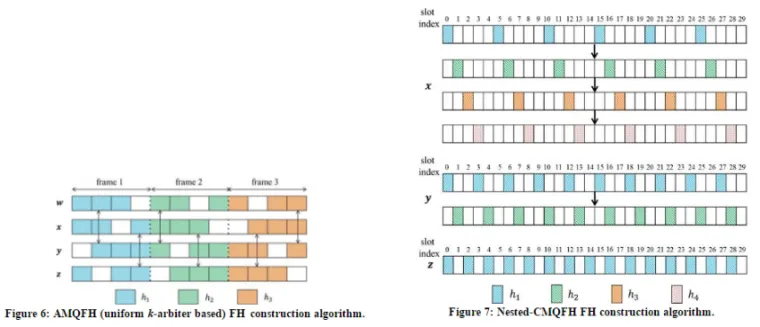
 Based on the above candidate quorum systems, we have been developing novel FH construction algorithms for multicast rendezvous. Issues that are being investigated include the criteria for selecting quorums and rendezvous channels. We are also analyzing and evaluating the security and performance aspects of these FH construction algorithms. An example of our FH construction algorithms is called AMQFH (k-arbiter based multicast quorum-based frequency hopping), and is shown in Figure 6 for four nodes (hence four FH sequences) and three frames. Figure 7 shows another example of an FH construction algorithm (called nested-CMQFH), which is based on the CRT quorum system. In this example, three FH sequences (x, y, and z) are generated. Similar to the nested grid-quorum-based rendezvous algorithm, nested-CMQFH uses multiple rendezvous channels per frame. However, the nesting degree is different for different FH sequences, so is the number of quorum slots in each FH sequence. The added nesting structure improves the rendezvous speed while maintaining a high HD.

 

3. Asynchronous Rendezvous in the Presence of Adverseries

Our third thrust is focused on adapting the parameters of a quorum-based rendezvous protocols in response to adversarial jamming. In general, we consider a setup in which multiple adversaries attempt to disrupt the rendezvous process. Different types of adversarial attacks are being investigated, including active/passive, insider/outsider, and reactive (adaptive)/non-reactive. These adversaries are assumed to have different levels of knowledge about the semantics of the rendezvous protocol. Moreover, we are examining the rendezvous problem under various network models: homogeneous/heterogeneous and synchronous/asynchronous. In here, by homogeneous we mean that all network nodes experience the same adversarial conditions on various frequency channels. Our aim is to design different algorithms for each setup, analyze the proposed algorithms, and evaluate them by means of simulations and/or experimentations. Sample tasks include the following:

Rendezvous Under Non-reactive External Jamming Attacks: In this task, we consider non-reactive jamming attacks, whereby adversaries do not adapt their strategies in response to actions taken by the rendezvousing nodes. The adversaries are assumed to be external devices that are not aware of any specific information about the semantics of the rendezvous protocol. We plan to consider different types of non-reactive jamming attacks. One type is the Markovian jamming attack, where the jamming signal follows a two-state Markov model.

To formalize the rendezvous problem under a Markovian jammer, we have formulated it as an optimization problem. This formulation can be applied to DSA systems. It can also be extended to other jamming models in which the state of the jammed channel can be modeled mathematically. Moreover, we have designed a centralized FH construction algorithm that achieves the minimum TTR while keeping the HD greater than a certain threshold. This algorithm will be used as a benchmark for distributed algorithms that we plan to develop. As a first step, we have customized the unicast and multicast rendezvous algorithms proposed for DSA systems to work in a general wireless network operating in the presence of Markovian jamming attacks. We have evaluated these algorithms under different jamming probabilities and different characteristics of the jamming signal.

Research issues that are being addressed include:

• Optimizing various parameters of the unicast and multicast algorithms to reduce the performance gap between these distributed algorithms and the centralized one.
• Studying other types of non-reactive outsider attacks, such as random jamming attacks, sweep jamming attacks, etc.

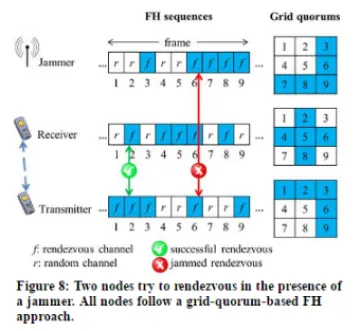
Rendezvous Under Reactive Insider Jamming Attacks: This part addresses the unicast and multicast rendezvous problem in the presence of a reactive insider jammer who is aware of the quorum-based FH design used by various nodes to rendezvous. The attacker adaptively selects its action based on observed actions of the legitimate nodes. It tries to prevent nodes from rendezvousing by maximizing the number of jammed rendezvous instances while minimizing the number of successful rendezvous instances. We are focusing first on the case of two nodes (a single wireless link), and later on we will investigate the anti-jamming multicast rendezvous problem. We study the rendezvous problem using different types of quorum systems, including grid, torus, and cyclic quorum systems. Figure 8 shows an example of a wireless link operating in the presence of a reactive jammer. All nodes (i.e., transmitter, receiver, and jammer) operate using a grid quorum-based FH approach. A successful rendezvous instance refers to a time slot where the transmitter and receiver are tuned to a rendezvous channel (channel f in Figure 8), while the jammer is tuned to a different channel. If the transmitter, receiver, and jammer are tuned to a common channel during the same slot, then this slot is called a jammed rendezvous slot. We formulated the interactions between the transmitter, receiver, and jammer as a three-player game. The formulation depends on the type of quorum system that is used for rendezvous. The transmitter and receiver try to maximize the number of successful rendezvous slots, while minimizing the number of jammed rendezvous slots. The jammer has the opposite objective. First, we are investigating the synchronous rendezvous game on a single channel (i.e., we assume that all players know the rendezvous channel). In this case, the game is to select the best quorum from the standpoint of each player. Next, we plan to investigate the case of synchronous and asynchronous rendezvous when various players do not know the rendezvous channels.

 

Research issues that are being addressed include:

• Studying the existence and uniqueness of the Nash equilibrium (NE) for the formulated games.
• Investigating the `best response' for each player that results in convergence to a NE (if one exists), and studying the convergence speed of the best-response update mechanisms (sequential/parallel) under the formulated games.
• Explore incentive-based (pricing) mechanisms for improving the efficiency of the resulting NEs.

Related Publications

• Mohammad J. Abdel-Rahman, Hanif Rahbari, and Marwan Krunz, “Rendezvous in Dynamic Spectrum Wireless Networks,” University of Arizona, Department of ECE, TR-UA-ECE-2013-2, May 2013.
• Mohammad J. Abdel-Rahman, Hanif Rahbari, Marwan Krunz, and Philippe Nain, “Fast and Secure Rendezvous Protocols for Mitigating Control Channel DoS Attacks,” Proc. of the IEEE INFOCOM 2013 Mini-Conference, Apr. 2013.
• Mohammad J. Abdel-Rahman, Hanif Rahbari, and Marwan Krunz, “Adaptive Frequency Hopping Algorithms for Multicast Rendezvous in DSA Networks,” Proc. of the IEEE DySPAN 2012 Conference (Technical Track), Oct. 2012.